Describe the Partition for Each of the Following Equivalence Relations

Let be the set of the real numbers. For example 123 R 523.

Solved Describe The Partition For Each Of The Following Chegg Com

Partitions and Equivalence Relations.

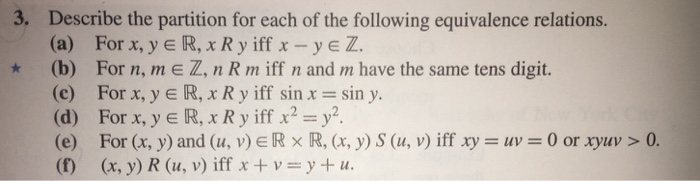
. Y x r for each b B r x y. For a given set of integers the relation of congruence modulo n. For any equivalence relation on a set A the set of all its equivalence classes is a partition of A The converse is also true.

Describe geometrically the members of this partition. If the relation is an equivalence relation describe the partition given by it. Describe the equivalence relation on each of the following sets with the given partition.

A partition of a set A is a collection of subsets of A that breaks up the set A into disjoint subsets. Pqℤq0 Define a relation R on S by. Now x R y iff x and y have the same decimal part.

XRy if xyxythe set of all real numbers The Answer to the Question. A For x y R x R y if x-y Z. If the relation is an equivalence relation describe the partition given by it.

Find step-by-step Discrete math solutions and your answer to the following textbook question. Let P be our partition. Reflexitivity 2 If ab R cd then ad.

Lets consider our relation. Will be the original set We have shown that the equivalence. Find the equivalence relation corresponding to each partition.

The equivalence relation defined by this partition is. 2 Let be the relation on R - 0 defined by x y if. Your description of each partition should have no redundancy and should not refer to the name of the relation.

So the distinct equivalence classes correspond precisely to the elements of 0 1. Ii Its symmetric because x-yy-x. As we run over each element of the set each element lies in one and only one of the equivalence classes so that the union of the equivalence classes will contain each element of the set ie.

The set of all such equivalence classes is the partition formed on R. Xy in R if x-y. For a given set of triangles the relation of is similar to and is congruent to shows equivalence.

Technically each pair of distinct subsets in the collection must be disjoint. X 2 y 2 r for each Hint. Hence if x-y.

The relation must be reflexive symmetric and transitive to be an equivalence relation. For each of the following equivalence relations describe the corre- sponding partition. That is each distinct equivalence class contains exactly one element of this interval.

An Important Equivalence Relation Let S be the set of fractions. Consequently we may consider a partition of a set as a way of dividing up into distinct non-overlapping pieces. A b R c d iff adbc.

To cover this possibility we need to use a more general notation. The sign of is equal to on a set of numbers. A partition can contain an infinite set of subsets.

Given a partition P on set A we can define an equivalence relation induced by the partition such that a sim b if. For all x y in mathbf R quad x A y Leftrightarrow x y. 1 For any fraction ab ab R ab since ab ba.

This relation is an equivalence relation. 1 prove that the relation is an equivalence relation and 2 describe the distinct equivalence classes of each relation. For all and.

Y x r is the equation of a line and x 2 y 2 r is the equation of a circle 3. A S XP X A b X 6 for all X P c X Y for all XY P X 6 Y 3 Need for the RST properties Any partition P has a corresponding equivalence relation. Ifthe relation is not an equivalence relation state why it fails to be one1 a b in R if a b2 m n in Q if mn 03 m n in Z if m n mod 2.

We introduce the following formal definition. I Its reflexive because a-a0. Determine whether or not the following relations are equivalence relationson the given set.

Then the three conditions are. There is a direct link between equivalence classes and partitions. Describe the partition for each of the following equivalence relations.

Equivalence relations can be explained in terms of the following examples. We then say that the collection of subsets is pairwise disjoint. Consider the relation on defined by if and only if --- that is if is an integer.

A B r x y. For example 13 39. Determine the following relation is an equivalence relation or not.

Is the absolute value relation defined on R as follows. 1 Let P be the set of all people and let be the relation on P defined by x y if and only if x and y have the same mother for all xy e P. In other words 1 4 and 5 are equivalence to each other 2 and 6 are equivalent and 3 is only equivalent to itself.

A N12 91011 99100101 999.

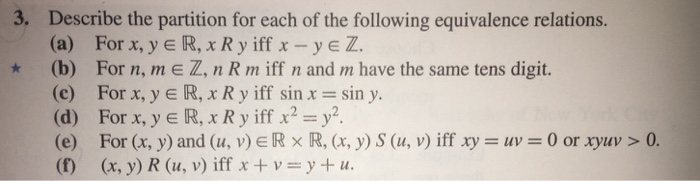
Describe The Partition For Each Of The Following Chegg Com

Solved B4 Prove That Each Of The Following Is An Chegg Com

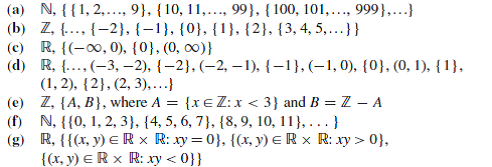
Solved Describe The Equivalence Relation On Each Of The Following Chegg Com